인턴하면서 전체적인 리딩을 해주시는 박사님께서 딥러닝에 필요한 수학을 기초부터 차근차근 해보자고 하셨다. 수학적인 베이스가 단단해야 나중에 더 어려운것도 이해할 수 있고, 더 나아가서 논문작성이나 구상에도 필수적이라고 하셔서 동의하고 진행하기로 하였다.
퍼셉트론이란
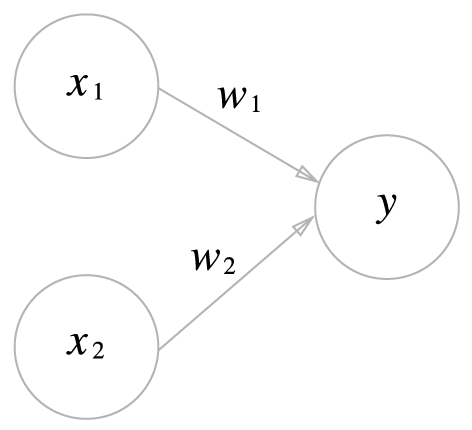
퍼셉트론은 다수의 신호를 입력으로 받아 하나의 신호를 출력합니다. 왼쪽 그림과 같이 두개의 입력신호(x1, x2)에 각각 가중치(w1, w2)가 부여되고, 입력값과 부여된 가중치가 곱해져서 어떠한 임계값을 넘어설 때만 1을 출력합니다. 이것을 수식으로 나타낸다면 밑에와 같을 것입니다. 즉 가중치는 각 입력 신호가 결과에 주는 영향력을 조절하는 요소로 작용합니다.

단순한 논리 회로
AND 게이트

그렇다면 위와 같은 AND 게이트를 퍼셉트론으로 표현하고 싶다면 어떻게 해야할까요? 위의 두개의 입력값 x1과 x2에 대한 가중치값 w1,w2와 임계값 θ를 정해야합니다. AND 게이트를 만족하는 (w1, w2, θ) 조합은 (0.5, 0.5, 0.7), (0.5, 0.5, 0.8) 등 무수히 많습니다.
NAND 게이트와 OR게이트

마찬가지로 NAND게이트와 OR게이트도 퍼셉트론으로 표현할때 (w1,w2,θ)을 설정해 주어서 표현할 수 있습니다.
이처럼 가중치값과 임계값을 적절히 조정해준다면 퍼셉트론으로 AND, NAND, OR게이트를 표현할 수 있습니다.
가중치와 편향도입
위에서 퍼셉트론을 수식으로 나타낸 식1은 다른 방식으로 수정할 수 있는데요,

사진의 식2와 같이 임계값 θ를 -b 치환하고 이항해준다면, 즉 b라는 편향을 도입해서 표현할 수 있습니다. 식을 다시 말해보자면 각각의 입력값에 가중치를 곱한값과 편향을 더한값이 0 초과이면 1, 0 이하이면 0이라는 것입니다.
이것을 또 다르게 말해본다면, 가중치에 해당하는 w1과 w2는 입력신호가 결과에 주는 영향력을 조절하는 매개변수이고, 편향 b는 뉴런이 얼마나 쉽게 활성화되느냐를 조절하는 매개변수인 것입니다.
퍼셉트론의 한계

OR 게이트의 경우를 생각해보면, 두개의 x1, x2로 OR 게이트에 해당하는 y값을 도출하려면 위 그림의 그래프처럼 직선을 그려 표현할 수 있습니다. 그렇다면 밑의 그림과 같은 XOR게이트를 하나의 직선을 그려서 표현할 수 있을까요?

XOR 게이트를 하나의 직선을 그려서 그래프 위에 y결과값이 0과 1이 되도록 영역을 나누는 것은 불가능 합니다. 직선이라는 제약사항을 없앤다면 밑의 그림처럼 나타낼 수 있는데요, 이처럼 한층의 퍼셉트론은 직선 하나로 나눈 영역만 표현할 수 있다는 한계를 가지고 있습니다.

OR게이트를 표현한 것처럼 직선의 영역을 선형 영역, XOR 게이트를 표현한곡선의 영역을 비선형 영역이라고 합니다.
다층 퍼셉트론
위에서 '단층' 퍼셉트론으로 XOR게이트를 표현할 수 없었습니다. 하지만 퍼셉트론을 여러층 쌓아서 '다층' 퍼셉트론을 구성한다면 XOR게이트도 표현할 수 있습니다.

위의 AND, NAND, OR게이트를 조합해서 밑의 그림과같이 XOR 게이트를 구성하고 진리표를 나타낼 수 있습니다.

뉴런을 이용한 퍼셉트론으로 표현한다면 다음과같이 나타낼 수 있습니다.

이처럼 퍼셉트론은 층을 쌓아서(깊게 하여) 더 다양한 것을 표현할 수 있습니다. 이렇게 퍼셉트론을 층층이 쌓아서 복잡한 회로를 구성하여 다양한 계산을 해낼 수 있습니다. NAND 게이트의 조합만으로 컴퓨터가 수행하는 일을 재현할 수 있다고 합니다.
'DL' 카테고리의 다른 글
| [DL 기초] 밑바닥부터 시작하는 딥러닝: 신경망(2) (0) | 2023.04.01 |
|---|---|
| [DL 기초] 밑바닥부터 시작하는 딥러닝: 신경망 (0) | 2023.03.25 |
| [Paper Review] Vision Transformer(ViT) 논문 정리 (0) | 2023.03.13 |
| [Paper Review] ResNet 논문 정리 (0) | 2023.03.06 |
| [Paper Review] GoogLeNet(Inception-v1) 논문 읽고 구현하기 with Pytorch (0) | 2023.02.01 |