[DL 기초] 밑바닥부터 시작하는 딥러닝: 신경망(2)
인턴하는 회사에서 진행하는 세미나 3주차의 과제로 사이토 고키의 밑바닥부터 시작하는 딥러닝의 3단원-다차원 배열 부분을 정리해 보고자합니다.
다차원 배열
2차원 배열은 행렬( matrix) 라고 부르고, 배열의 가로를 행, 세로 방향을 열이라고 합니다.

행렬의 곱
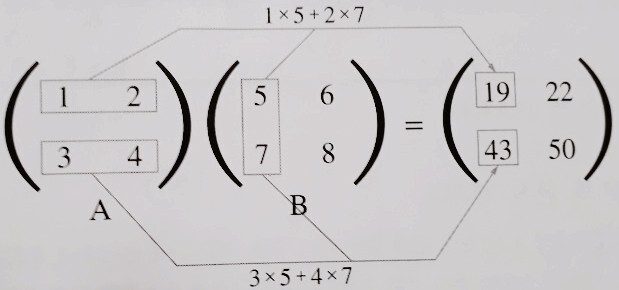
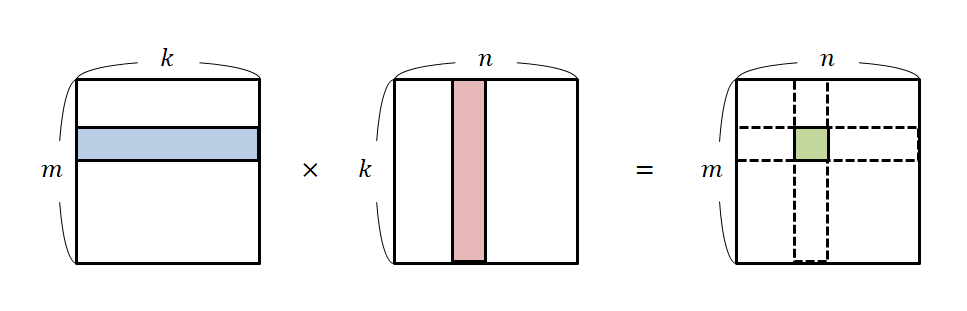
행렬의 곱은 다음과 같이 진행하면 됩니다. 왼쪽 행렬의 행과 오른쪽 행렬의 열을 원소별로 곱하고 더해줍니다. 다만 여기서 조심해줘야할것은 곱하는 두 행렬의 차원입니다. 이를테면 A행렬과 B행렬을 곱해준다고 하면, A행렬의 열 수와 B행렬의 행 수가 일치해야합니다.
신경망에서의 행렬곱
그렇다면 신경망에서의 행렬곱에 대해서 생각해 보겠습니다. 다음과같이 x1과 x2가 입력값(1x2) 이고 2x3짜리 가중치 행렬이 있다면 두 행렬의 곱은 1x3의 차원을 가집니다. 즉, 3개의 y1,y2,y3를 결과값으로 내놓게 되는것입니다.

3층 신경망 구성하기
책에서는 3층 신경망에서 수행되는 입력에서 출력까지의 순방향처리를 구현했습니다.

위와 같은 3층 신경망 입니다. 밑의 그림에서는 편향이 입력단에 추가되었습니다. 입력단의 x1, x2, 1(편향)은 가중치에 곱해져서 1층의 첫번째 뉴런의 값으로 도출이 되는데요, 그 수식은 밑의 두번째 그림과 같습니다. 그리고 그것을 행렬을 곱을 이용한다면 입력행렬 X, 가중치 행렬 W, 1층 뉴런의 값들의 행렬 A, 편향 B로 나타낼수 있습니다.



이때 A, X, W, B행렬은 밑에와 같이 나타낼수있는데요, 정확히 차원이 일치하는것을 확인할 수 있습니다.

이후과정으로 1층 뉴런에서 활성화함수 처리가 진행됩니다.

위의 과정과 동일하게 1층 뉴런층에서 2층 뉴런층으로 그리고 최종 출력층으로 순방향연산이 진행됩니다.

이렇게 마지막 출력단까지 연산이 진행되는데요, 한가지 생각해야할것은 출력층의 활성화함수는 풀고자 하는 문제의 성질에 맞게 정해야한다는 것입니다. 회귀에서는 항등함수를, 2클래스 분류에서는 시그모이드함수를, 다중 클래스 분류에서는 소프트 맥수함수를 사용한다고 합니다.
소프트맥스 함수

위의 소프트 맥스 함수 수식에서 exp()는 지수함수를 뜻합니다. n은 출력층의 뉴런수, yk는 k번째 출력을 의미합니다. 분자는 입력 신호 ak의 지수함수, 분모는 모든 입력 신호의 지수함수 합으로 구성됩니다.

따라서 소프트맥스 함수의 출력은 모든 입력 신호로부터 영향을 받는다고 할 수 있습니다.

이렇게 위의 그림처럼 소프트맥스 함수의 출력은 0에서 1.0사이의 실수입니다. 또한 소프트맥스 함수 출력의 총합은 1입니다. 이러한 성질 덕분에 소프트맥스 함수의 출력은 확률로 해석할 수 있습니다.
이를테면 위의 그림과 같이 1번째 클래스일 확률을 3퍼센트, 2번째 클래스일 확률은 82퍼센트, 3번째 클래스일 확률을 15퍼센트입니다. 이렇게 소프트맥스 함수를 이용함으로써 문제를 확률적으로 대응할 수 있습니다. 다만, 소프트맥스 함수를 적용해도 각 원소의 대소관계는 변하지 않습니다. 즉, 소프트 맥스함수를 지나지 전 a값에서와 지난후 y값에서의 대소관계는 변하지 않습니다. 따라서 최근에는 지수함수 계산에 드는 자원 낭비를 줄이고자 출력층의 소프트맥스 함수를 생력한다고 합니다.
손글씨 숫자 인식
위에서 공부한 신경망을 손글씨 숫자분류에 적용해볼수 있습니다. 책에서는 먼저 학습이 아닌 추론과정을 설명하고 있습니다. 밑의 그림과 같이 28x28 크기의 MNIST 데이터 셋을 1차원으로 Flatten과 Normalize해준후 신경망에 순전파를 시킵니다. 출력층에서는 softmax함수를 지나 예측한 레이블을 결과값으로 내놓습니다.

배치처리
위의 사진에서는 MNIST 이미지 1장에 대해서 신경망 추론을 진행하였고, 그것의 배열형상의 추이로 나타낸다면 다음과 같습니다.

그렇다면 이미지를 여러장을 한꺼번에 신경망에 입력하는 경우를 생각해본다면 다음과 같을 것입니다. 즉, 10000개를 한꺼번에 신경망에 입력했다면, 결과값으로는 10000개의 이미지에 대한 10개의 Label에 대한 Softmax값 즉 확률값이 나올것입니다. 이처럼 하나로 묶은 입력 데이터를 배치(batch)라고 합니다. 이렇게 배치처리하는 것은 컴퓨터로 연산을 할때 큰 이점을 준다고하는데, 이미지 1장당 처리 시간을 대폭 줄여준다고 합니다. 배치 처리를 함으로써 큰 배열로 이뤄진 연산을 하게 되는데, 컴퓨터에서는 큰 배열을 한꺼번에 계산하는것이 분할된 작은 배열을 여러번 계산하는것보다 빠르기 때문입니다.
